Mental Mathematics

Every Transition to Algebra lesson (except the very first) begins with a brief (5-minute), lively, and highly-focused Mental Mathematics activity. These exercises are strategically chosen to:

• build mastery of basic number facts,
• increase students’ capacity to juggle multiple pieces of mathematical information simultaneously, and
• develop an intuitive, “common sense feel” for basic algebraic properties of operations.

Most times, these are verbal exercises with the whole class; sometimes they take other formats such as chorusing one row of students at a time or alternating between the whole class and individual students (without embarrassing that student).

Lesson Launch

Most lessons begin with an introductory activity to set the tone for the class. The goal is not for students to be able to demonstrate mastery after the launch. Instead, students should feel curious enough to proceed on their own, and the launch prepares them to do this by introducing a new puzzle or clarifying instructions for new problem types. Since this is only the launch, it does not give away the punch line. Students find their way to the goals of the lesson through solving more problems on their own and in groups, by reading dialogues together, and through teacher guidance in class discussions.

Student Problem Solving

Students need time to solve problems on their own, individually and with partners or small groups. Both kinds of work are essential complements to the work they do under teacher guidance. As students work together, the teacher listens for evidence of mathematical thinking that can be highlighted during a subsequent class discussion. Group work allows students to engage with the materials in a less formal, lower stakes setting where they can explore mathematical thinking without the pressure of the teacher’s knowledge of the subject. This benefits all students and particularly those students whose first language is not English, who may struggle to communicate with adults but feel more comfortable communicating with their peers. In group-work, students with different learning styles collaborate to build a common understanding and grapple with the mathematics in a way that the lecture format doesn’t allow. Struggling students can contribute to discussions even if they can’t compute quickly or come to the correct answer reliably; for instance, they may notice a connection, clue, or question that others hadn’t thought of. And students with a better understanding of the content strengthen their knowledge as they explain their thinking to their peers.

Student Dialogues

Student dialogues (labeled “Thinking out Loud”) appear several times in each unit. These scripts model mathematical discussion, address common confusions and misunderstandings, and encourage academic and mathematical language. The three students who appear in these dialogues – Michael, Lena, and Jay – are all good students with distinctive mathematical personalities.

• Michael asks the most questions and often seeks clarity and validation of his understanding.
• Lena is generally confident and follows the methods learned in school.
• Jay tends to see problems in creative ways and shares alternative ideas for working through problems.

Pilot teachers have managed the dialogues in various ways. Some just have students read them out loud in class. Others enjoy acting. Students in Chicago classrooms even videotaped their readings and posted them on YouTube!

Class Discussions

Allowing students to discuss their thinking is crucial to the success of the Transition to Algebra curriculum. Class discussions (labeled “Discussing Together”), support students in making sense of their own work solving problems, understanding other students’ approaches and ways of thinking, and synthesizing their own thinking and understanding. The discussions also set the tone for the class – one which honors the process of learning math, not just correct answers. In class discussions, good thinking is rewarded by thoughtful discourse, and even struggling students can meaningfully contribute. Discussions are also an opportunity for the teacher to encourage a culture that celebrates any answer (right or wrong) that is reached by good mathematical thinking. Having students discuss their thinking will help them develop the clear communication necessary for word problems on tests and other assessments, and they can be fun way to check-in with kids and to catch misconceptions and other errors.

Explorations

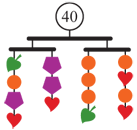
TTA includes open-ended, student-directed explorations and many are designed to be done using manipulatives. Manipulatives lower the barriers for entering problems and allow students to arrange and organize information in their own way, which encourages thinking that is not as easily achieved by drawing or writing.

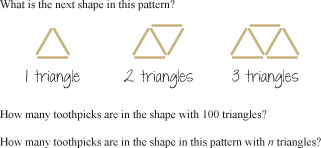
The Explorations are designed so that all students can enter into the problem easily, though the mathematics can potentially go far beyond that entry point. For example, these explorations may lead students into discussions about combinatorics, the Fibonacci sequence, triangular numbers, and so on, but these are not the essence of the activity. The point is not the results of the exploration, but learning how to be a mathematical explorer.

The question “Am I done?” is non-trivial in explorations, as in all problem-solving.  In day-to-day mathematics, students are rarely faced with problems for which it is unclear whether all the cases and possibilities have been considered, yet it is only in these contexts that students have sufficient motivation to develop a systematic process for analyzing their process. 

Assessments

The Transition to Algebra curriculum includes two types of assessments: Snapshot Check-ins and Unit Assessments. Primarily a formative assessment tool, the mid-unit Snapshot Check-ins offer teachers and students an opportunity to assess how well students are integrating new content before moving on. The primary purpose of these Check-ins is to gauge what students know, discuss any difficulties as a class or individually, and to learn from those discussions. Teachers may wish to have students discuss the problems and/or use this feedback tool to help select problems for additional practice. The Unit Assessments summatively evaluate students’ success with the Learning Goals of each unit.

Additional Practice Materials

Optional additional practice materials are included with each lesson for use at any time in the unit. These materials are versatile, so teachers can direct students to specific exercises according to their individual learning needs. Teachers may elect to assign them as homework, review one or two in class, or assign a whole page on a day with a substitute teacher. Additional Practice problems at the end of the unit address all fundamental ideas from the unit and provide review for the Unit Assessment.