Mathematical puzzles take on a central role in Transition to Algebra as a device to develop problem-solving expertise and stamina and to undo a brittle and rule-bound perception of mathematics that many students bring and that gets in the way of their solving unfamiliar problems.
View a printable sample page of our puzzles. Or click the iPuzzle tab above form information and access for our puzzle apps.
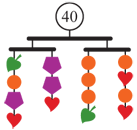
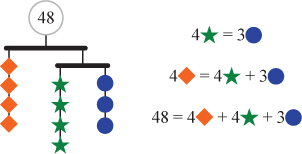Mobile Puzzles typically present multiple balanced collections of objects whose weights must be determined by the puzzler. The imagery helps students build the logic of balancing equations, an intuitive understanding of substitution, and common-sense strategies that become the foundation for the standard algebraic “moves” involved in solving equations and systems of equations. These are essentially pictorial representations of systems of several simultaneous equations in two or more variables. Such puzzles thereby help students simultaneously grasp the concept and role of a variable and develop the logic of algebraic manipulation. Gradually, shapes are replaced with variables, strings of shapes are replaced by algebraic expressions, and finally sections of mobiles are translated into equations.
Truth Puzzles require students to deduce reliable information from statements whose truth value is not initially known. Much of mathematics is about figuring out when, or whether, a statement is true or false. The statement x2 = 9 is true only when x = 3 or x = -3; the statement x + 1 = x + 2 is false, no matter what x might be. The ability to determine the truth value of statements is essential to understanding if a number is a solution of an equation or if a point is on a graph.
Truth puzzles are a familiar staple of recreational mathematics, here presented as the stories of strange little creatures called Beebos. Beebos come from two different families, Liars and Truthtellers. Beebos in the Liar family always lie. Beebos from the Truthteller family always tell the truth, no matter what. The tricky thing is, you can’t tell just by looking at them which family they are from.
While the content of these puzzles seems to be “just logic,” these puzzles turn out to be particularly rich vehicles for developing the academic language around mathematical reasoning. Because answers are not “just computations,” students are spontaneously drawn to explain how they know what they know, and they readily acquire if…then language and the explanatory strategy of singling out cases.
Order Puzzles present clues that are, in effect, systems of simultaneous inequalities about age, height, location, and so on, from which students must determine the order of a set of objects or answer questions about the position of one element, the relationship between two elements, or which element(s) might be in a particular position. As with the truth puzzles, students are generally drawn to explain how they know what they know and consequently develop language to explain their reasoning.
Four piano students—Ashley, Brandon, Cassie, and Damian—will give a recital. Cassie insists on playing immediately after Brandon. Ashley might be late, so she can’t go first. Damian and Ashley are playing the same piece, so at least one other player must come between them. Help their teacher figure out in what order to have them perform.
Where-Am-I? Puzzles are another variant of number-line-based puzzles. Even a relatively simple puzzle like “I am twice as far from 5 as I am from 6. Where am I?” has more than one solution and requires students to decide exactly how many solutions and how to find them. These evolve into various two-dimensional Where-Am-I? puzzles on the coordinate plane.
Who-Am-I? Puzzles give clues about a multi-digit mystery number that students try to identify. These puzzles build working memory and the ability to coordinate multiple pieces of information and draw logical conclusions. They also strengthen academic and mathematical vocabulary as well as the interpretation of symbolic language. The mathematical content of puzzle clues can include place value, divisibility, primes, parity, squares, magnitude, and so on. Clues can also be written as algebraic statements about the relationships among the digits and can connect to particular algebra topics such as this puzzle which requests a pair of numbers with a sum of 11 and a product of 24, just as in factoring x2 + 11x + 24.
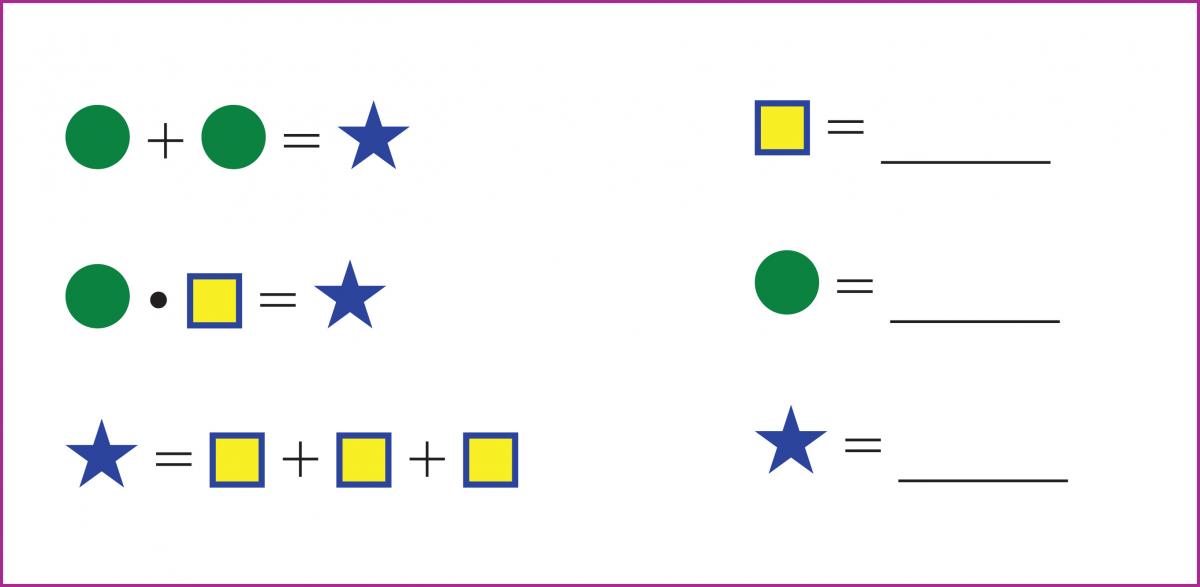
Mystery Number Puzzles present systems of equations or inequalities in a fun context that focuses on finding solutions not through rules but by reasoning logically about the properties of numbers and operations. Alone or in combination, the clues place restrictions on the values of the variables to help focus on these properties. Like the Who-Am-I? puzzles, Mystery Number puzzles build working memory and the ability to coordinate multiple pieces of information, as this example—essentially a system of simultaneous equations—shows.
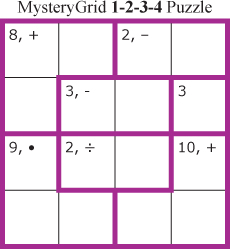MysteryGrid Puzzles that use only integers are well known under a variety of names including Calcudoku and KenKen™ puzzles. The integer-only variety shown here specifies certain numbers that can be written—in this case only 1, 2, 3, and 4—and follows a Sudoku-like rule that no number can be repeated in any row or column. Further, each “cage”—a region surrounded by a dark boundary—contains a target and usually an operation. Using only that operation, the numbers that may be written within the cells of that cage must exactly reach the target. The solution is unique, but there are many ways to start. For example, the bottom left cage requires that 9 be made by multiplication. Therefore the only allowable numbers that will work are 3, 1, and 3, with the 1 in the corner. That then tells us the top two numbers in the left hand column must be 2 and 4, though we don’t yet know what order to write them in. A look at the second-from-top row will help. Because “3, –” must contain 4 and 1 (in some order), 4 cannot also be in the left-hand cell of that row, so now we know the entire left-hand column in order.
Transition to Algebra extends this puzzle type to use varied sets of terms in each box, such as primes, fractions, or algebraic expressions (such as 1, x, x + 1, and x2).
While exercising basic arithmetic and algebraic skills including the four operations and factoring, puzzles of this type also strengthen some of the cognitive tools needed for success in algebra: tracking and managing multiple constraints, mathematical stamina, and reasoning strategically rather than guessing.