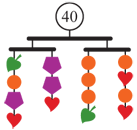
One important purpose of learning mathematics is to develop useful, analytic, quantitative, logical ways of looking at the world and thinking about things. When mathematical ways of thinking begin to become automatic—not just ways one can use, but ways one is likely to use—it is reasonable to call them habits: mathematical habits of mind.

The Standards for Mathematical Practice (SMP) listed in the Common Core State Standards (CCSS) are one way of organizing and presenting a subset of mathematical habits of mind that are essential for mathematical proficiency. Transition to Algebra focuses on algebraic aspects of five of these: puzzling and persevering, seeking and using structure, using tools strategically, describing repeated reasoning, and communicating with precision. Transition to Algebra is designed to develop these algebraic habits by fostering and building on the common-sense logic that students bring.

Puzzling and Persevering:

“Mathematically proficient students start by explaining to themselves the meaning of a problem and looking for entry points to its solution. They ... plan a solution pathway rather than simply jumping into a solution attempt [and they] monitor and evaluate their progress and change course if necessary...” (CCSS, MP1)

Students often see mathematics as a collection of rules to know and follow. Genuine problems—in school and out—are not so cut and dried. Standardized tests also give problems that require students to think beyond the rules. Even ordinary word problems require students to figure out where to start and what to do next. There is no “formula” for how to do that and that is one reason why students find word problems difficult. Puzzles place that particular skill—figuring out where to start—front and center. The puzzles in Transition to Algebra have been chosen strategically to support mathematical ways of thinking essential in algebra.

Seeking and Using Structure:

“Mathematically proficient students look closely to discern a pattern or structure... They also can step back for an overview and shift perspective. They can see complicated things, such as some algebraic expressions, as single objects or as being composed of several objects...” (CCSS, MP7)

Students in beginning algebra are often taught to solve equations like 2(x + 3) + 4 = 24 by going through a particular set of steps written in a particular way. On successive lines, they write the original equation, -4 below each side, a new equation, ÷2 below each side, a new equation, and so on. That method works for all first-year algebra cases and helps students “see the steps.” But it doesn’t encourage students to “see beyond the trees” and perceive the overall structure. Both are necessary. Seeing the structure helps students see the logic of algebra; it often also makes calculation much easier.

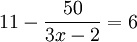Consider the example to the right. Proceeding in the conventional way is much, much harder than seeing the equation as 11 minus “something” is 6 and concluding that the “something” (the  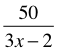) equals 5. We can read that as “fifty divided by something” is 5. So, that “something” (the 3x – 2) is 10. That leaves 3x − 2 = 10, which is easier to solve.

Using Tools Strategically:

“[This entails] knowing and flexibly using different properties of operations and objects.” (CCSS, MP2)

“[Mathematically proficient students] ...identify important quantities in a practical situation and map their relationships using such tools as diagrams, two-way tables, graphs, flowcharts and formulas. They…reflect on whether the results make sense...” (CCSS, MP4)

“[They] consider the available tools when solving a mathematical problem [and] are sufficiently familiar with tools appropriate for their grade or course to make sound decisions about when each of these tools might be helpful, recognizing both the insight to be gained and their limitations.” (CCSS, MP5)

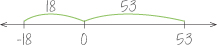
Good use of tools requires a certain amount of reasoning about and picturing results before they are fully derived. In arithmetic and algebra, that means reasoning about calculations and operations and predicting how part or all of a calculation would go without necessarily carrying it out. For example, if students picture how -18 – 53 would look on the number line, and if they understand the calculation as asking for the total distance and sign, they can perform that calculation without needing a case-structured set of “rules.” Using only this reasoning, students can say whether the result is positive or negative or whether the “18” and “53” should be added or subtracted. This image of the number line clarifies that two distances are being added. The sign comes from subtracting a larger number (53) from a smaller one (-18), which is what they’ve always known with positive numbers.

Describing Repeated Reasoning:

“Mathematically proficient students notice if calculations are repeated, and look both for general methods and for shortcuts. ... As they work to solve a problem, [they] maintain oversight of the process, while attending to the details. They continually evaluate the reasonableness of their intermediate results.” (CCSS, MP8)

This habit manifests when students uncover a pattern, explore its mathematics, and develop a generic way (often an algebraic expression or equation) to describe it. The practice of seeking and articulating regularity is a cornerstone of algebraic thinking. Consider the following problem:

Asher has a part-time job, working 20 hours a week. He does so well that he is hired full time (40 hours a week) and he is also given a $1 per hour raise. He is really happy, because now he will make $270 more each week than he made before. How much was he making per-hour before the raise? How much is he making now?

Many students who can solve the algebraic equation that represents this problem can’t generate that equation. Transition to Algebra teaches students how they can generate an equation by guessing a starting wage and calculating the weekly earnings before and after the promotion, then repeating that process for a different arbitrary guess. The goal is not for students to find an answer by guesswork, trial and error, or approximation and adjustment. The goal is for them to notice the regularity in the operations they use to check their guesses. Then students generalize the process by “calculating" and comparing the two different weekly earnings when they’ve “guessed" that Asher used to make x dollars per hour. His old earnings, then, are 20x and his new earnings are 40(x + 1). He earns 270 more now than before: 40(x + 1) - 20x = 270. This is the equation they need to solve.

Communicating with Precision:

“Mathematically proficient students … justify their conclusions, communicate them to others, and respond to the arguments of others. They … distinguish correct logic or reasoning from that which is flawed, and—if there is a flaw in an argument—explain what it is.” (CCSS, MP3)

“Mathematically proficient students try to communicate precisely to others. They try to use clear definitions in discussion with others and in their own reasoning. They state the meaning of the symbols they choose, including using the equal sign consistently and appropriately. They are careful about specifying units of measure, and labeling axes to clarify the correspondence with quantities in a problem.” (CCSS, MP6)

As students develop mathematical language, they learn to use algebraic notation to express what they already know and to translate among words, symbols, and diagrams. Clear communication also requires the refinement of academic language as students explain their reasoning and solutions. Along with some new specifically mathematical vocabulary, this includes the use of:

• quantifiers (all, some, always, sometimes, never, any, for each, only etc.)
• combination and negation (not, or, and)
• conditionals (if…then…, whenever, if not, etc.)